
A avaliação de imóveis é um processo complexo que utiliza diversos métodos para determinar o valor de uma propriedade. Ao recorrer à inferência estatística, adotamos a análise de regressão para modelar o mercado imobiliário, fundamentando-nos em um estudo aprofundado do comportamento do mercado
A inferência estatística na avaliação de imóveis
A inferência estatística engloba um conjunto de métodos destinados a extrair conclusões ou realizar previsões sobre uma população, baseando-se em dados amostrais. Essa abordagem possibilita a estimativa de parâmetros, o teste de hipóteses e a modelagem de relações entre variáveis, empregando a teoria da probabilidade para mensurar a incerteza associada a essas inferências.
No contexto da avaliação de imóveis, esforçamo-nos para determinar o valor de uma propriedade específica, utilizando como referência a média dos preços vigentes no mercado imobiliário e a comparação com imóveis similares ao objeto de nossa avaliação. Contudo, essa estratégia supõe um conhecimento completo dos valores de mercado, uma premissa muitas vezes inviável.
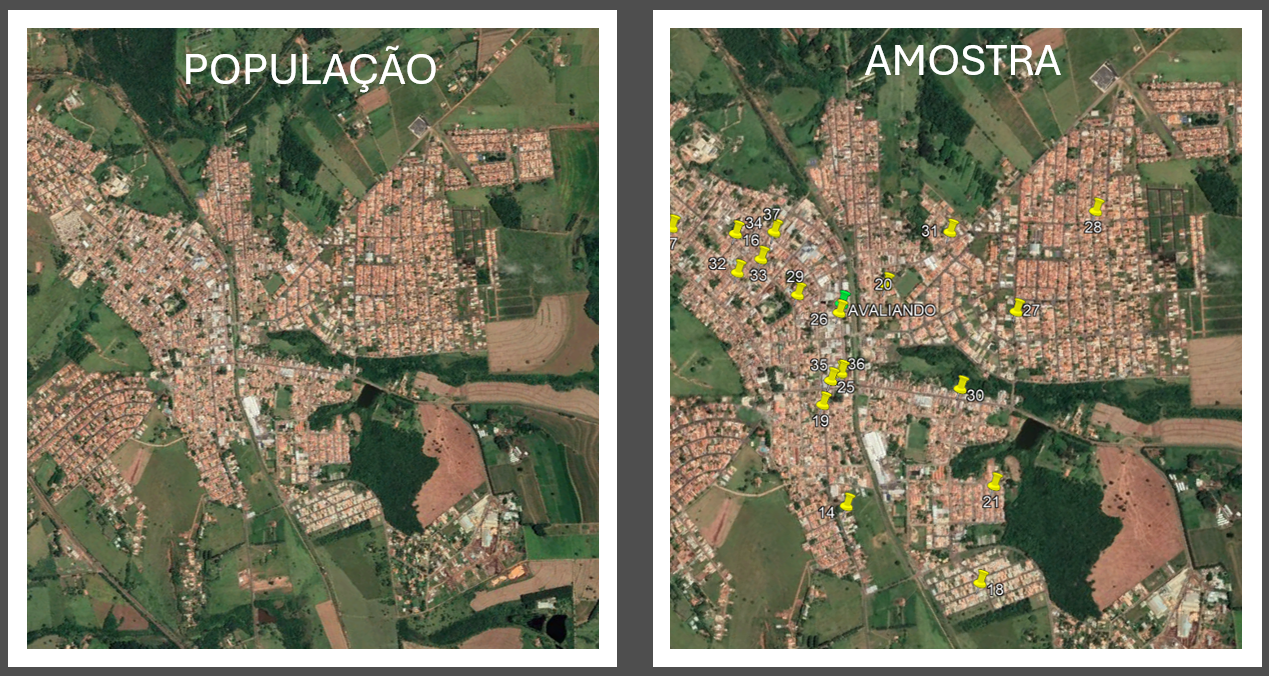
O que realmente está ao nosso alcance é o acesso a somente uma fração da população total, referida como amostra. Com base nessa amostra, adotamos técnicas de inferência estatística para estimar valores e parâmetros. Este processo nos permite, de forma embasada, fazer generalizações sobre o mercado inteiro a partir de uma parcela dos dados disponíveis, contribuindo para a realização de avaliações imobiliárias mais precisas.
A Regressão Linear
Na avaliação de imóvel por inferência estatística a regressão linear é uma ferramenta estatística que permite explicar a variação encontrada nos preços dos imóveis que compõem uma amostra. Em geral, essas variações ocorrem por diferenças físicas nos imóveis, sua localização ou fatores socioeconômicos
Exemplo didático de regressão linear
A seguir, apresentamos um exemplo sobre a aplicação da regressão linear na avaliação de imóveis. Vamos considerar uma cidade hipotética na qual precisamos avaliar uma casa. Idealmente, coletaríamos todas as informações sobre as casas semelhantes na cidade, o que, como já vimos, seria impossível. Ao invés disso, vamos coletar informações de 6 casas (dados amostrais) para, a partir desses dados, entender como seria o comportamento da população (que, no nosso caso, é o mercado imobiliário).
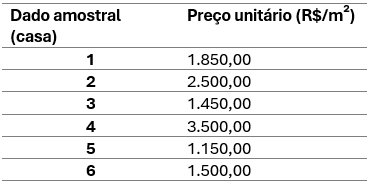
Dessa pesquisa, obtemos uma média, que, no caso mencionado, foi de R$ 1.991,67. Esse valor, isoladamente, não nos oferece muita informação; na verdade, ele só seria útil se todas as casas fossem idênticas, o que não é o caso.
Variação em torno da média
Em qualquer amostra aleatória, teremos uma variação de preços em torno da média. Essa variação é chamada de variação total e contém as explicações das variáveis que formam os preços dos imóveis, além de eventuais erros de medição.
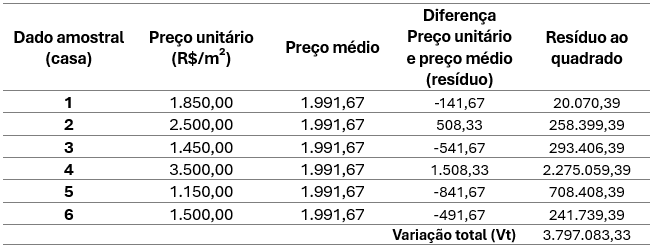
O método para o cálculo da variação total (Vt) é dado pelo quadrado da diferença entre cada preço e a média, o que fica mais fácil quando colocamos isso em uma tabela:
Agora, é importante demonstrar quanto dessa variação é explicada por atributos físicos ou outras características dos imóveis pesquisados. Para isso, vamos introduzir uma nova variável à nossa pesquisa: a área construída.
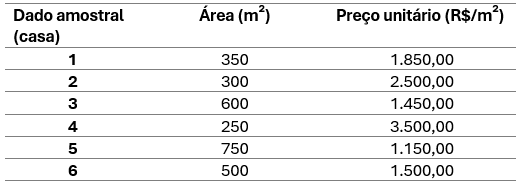
Deste modo, podemos até traçar um gráfico da área pelo preço:
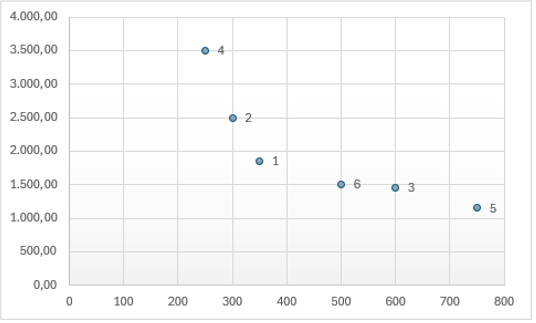
No gráfico anterior, podemos inserir a mesma análise da tabela 01, calculando as distancias de cada ponto até a média calculada:
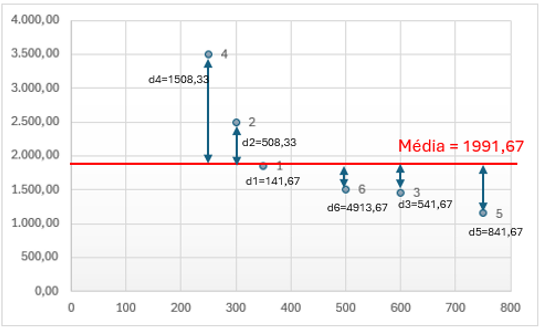
Vt = d1² + d2² + d3² +d4 ²+ d5²+ d6² = 3.797.083,33
Graficamente, o que temos é uma reta com o coeficiente angular nulo e com o intercepto igual a média aritmética.
Mínimos Quadrados
Agora, podemos supor que exista outra reta capaz de explicar essa variação de preços de maneira mais eficiente. Quando dizemos "explicar melhor", estamos buscando uma reta que apresente uma variação total (Vt) o mais baixa possível. A essa técnica, damos o nome de Mínimos Quadrados.
Planejo escrever outro artigo detalhando essa técnica. Por enquanto, é importante entender que essa nova equação de reta minimiza o somatório do quadrado da distância dos pontos até a reta, tornando essa distância a menor possível.
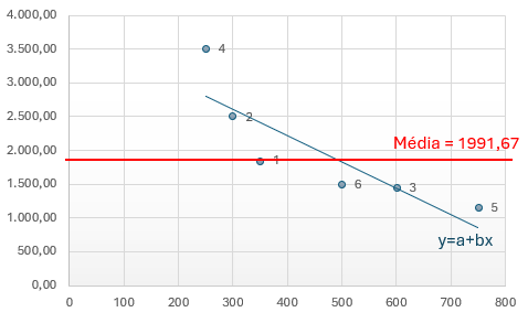
Em resumo, a regressão linear modela a relação entre uma variável dependente (o valor do imóvel) e uma ou mais variáveis independentes (características do imóvel, como localização, área, número de quartos, etc.).
O objetivo é encontrar a reta que melhor se ajusta aos dados, minimizando a soma dos quadrados das diferenças entre os valores observados nos dados e os valores previstos pela linha de regressão.
Passo a passo na Avaliação de Imóvel por inferência
Escolha das variáveis
Inicialmente, selecionam-se as características do imóvel que influenciam seu valor. Essas variáveis podem incluir a localização, o tamanho, a idade da construção, a qualidade dos acabamentos, a infraestrutura local, entre outros fatores.
Modelagem
Utiliza-se a regressão linear, de modo semelhante ao explicado anteriormente, para estabelecer a relação quantitativa entre o valor do imóvel (variável dependente) e as características selecionadas (variáveis independentes). Isso resulta em uma equação que prediz o valor do imóvel com base nessas variáveis.
Testes de Hipótese
Após a realização da regressão, surge a questão de como determinar se o modelo está correto ou não, ou seja, se as variáveis escolhidas estão efetivamente explicando as variações dos preços. Para responder a isso, recorre-se aos testes de hipótese, que são empregados para validar as suposições feitas durante a avaliação de imóveis por meio da inferência estatística. Esses testes possibilitam que os avaliadores verifiquem a significância das variáveis independentes no modelo de regressão linear, determinando se essas características possuem um impacto estatisticamente significativo no valor do imóvel. A aplicação dos Testes de Hipótese envolve os seguintes passos:
Formulação do teste de hipótese
Ao aplicar os Testes de Hipótese, segue-se a seguinte etapa inicial: define-se uma hipótese nula (H0), que geralmente afirma que não existe relação entre a variável dependente e as variáveis independentes. Paralelamente, a hipótese alternativa (H1) sugere a existência de uma relação significativa.
Nível de significância
Determina-se um nível de significância previsto em norma, o qual corresponde à probabilidade de rejeitar a hipótese nula quando ela é de fato verdadeira. No contexto do laudo de avaliação de imóvel, é o grau de precisão requerido que vai estabelecer o nível de significância, conforme estipula a NBR 14653.
Calculam-se os valores p para as variáveis independentes. Se o valor p for menor que o nível de significância estabelecido, rejeita-se a hipótese nula, indicando que a variável exerce um impacto significativo no valor do imóvel.
Portanto, o teste de hipótese é fundamental para determinar a relevância do modelo e a influência necessária das variáveis consideradas na composição do valor do imóvel.
Considerações finais
A inferência estatística, um é particularmente valiosa quando se lida com uma amostra heterogenea de propriedades. Essa abordagem leva em consideração as características únicas de cada imóvel, ajustando o seu valor com base em especificidades que podem influenciar significativamente a sua avaliação, e realiza comparações com outros imóveis sob condições de mercado equivalentes.
A necessidade de avaliação de imóveis por inferência estatística em bancos e órgãos públicos destaca a importância dessa metodologia. Instituições financeiras renomadas, como o Banco do Brasil, a Caixa Econômica Federal, o BNDES e o BDMG, bem como diversos órgãos públicos, requerem avaliações baseadas em inferência estatística. Esse pré-requisito promove transparência, justiça e precisão nas avaliações de propriedades, servindo a propósitos de financiamento, investimento e regulamentação e sua adoção assegura uma avaliação mais precisa e equitativa, refletindo o verdadeiro valor de mercado dos imóveis.
Veja também:

